
So essentially the bandwidth limitations of each transistor stage are ignored. First order filters are much easier to deal with in closed loop designs than higher order feedback with issues with instability, oscillations, ringing, overshoot. This is performed by an small integrating capacitor in the intermediate stages of the Op Amp.īy swamping (shunting) the gain of the amplifiers well below what they are capable of, means that the frequency limitations of each transistor stage are replaced with an ideal amplifier and an integrator. The DC low pass filter with a breakpoint of 20 Hz and a gain of 120 dB is no accident.
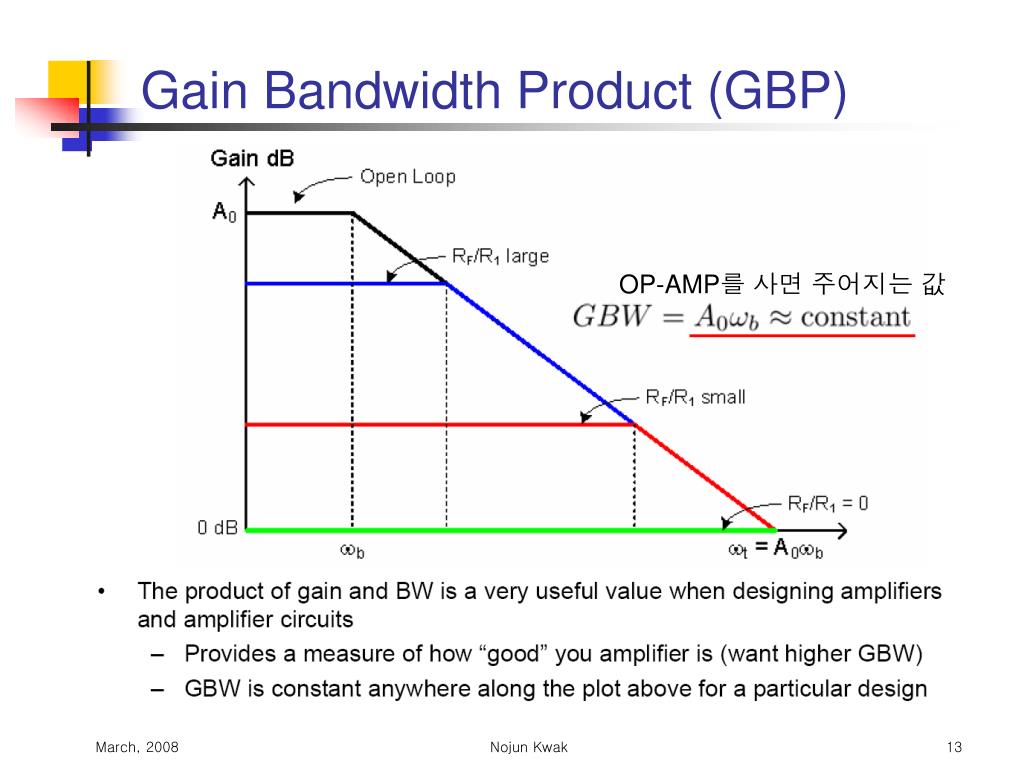
In the above diagram the loop gain for small frequencies is 120dB-40dB=80dB and rolls off with 20dB/dec until it reaches 0dB at w=wo (2Pi*220kHz).Ĭomment (with respect to the contribution from James): The inverse feedback factor 1/k is sometimes called "noise gain".

Note that the region between the 1/k line and the Aol response gives you the loop gain in dB - and at w=wo we have unity loop gain.

What I cannot understand is why can we find/use the close-loop gain on the bode plot of "Open-loop gain vs frequency" ?Įxample: Non-inverting amplifier with closed-loop gain:Īcl=Aol/(1+kAol)=1/ (with open-loop gain Aol and feedback factor k.)įor low frequencies (Aol>k and 1/Aol>wo the horizontal line (1/k) is above the Aol curve - now we have 1/k>Aol or k<

 0 kommentar(er)
0 kommentar(er)
